ГИПОЦИКЛОИДЫ И ЭПИЦИКЛОИДЫ, общее название кривых, описываемых произвольной точкой окружности, катящейся без скольжения по неподвижной окружности. Если касание обеих окружностей внутреннее, то соответствующие 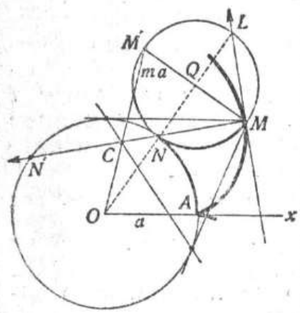 кривые называются гипоциклоидами, а если оно внешнее, — то эпициклоидами. Г. и э. принадлежат к числу так называемых рулетт (см.) и имеют важные приложения в теории механизмов.
кривые называются гипоциклоидами, а если оно внешнее, — то эпициклоидами. Г. и э. принадлежат к числу так называемых рулетт (см.) и имеют важные приложения в теории механизмов.
Если в начале движения точка , описывающая Г., занимает положение (см. рис.), то во всякий момент движения дуга равна дуге (это геометрическое выражение того, что движение происходит без скольжения). Параметром, определяющим данную Г., является отношение угла к углу , численно рапное обратному отношению радиусов обеих окружностей; это отношение имеет отрицательное значение, когда касание внутреннее, и положительное, когда касание внешнее. Т. о., Г. соответствуют отрицательным, эпициклоиды — положительным значениям . При , если предположить, что с приближением к нулю радиус неподвижной окружности а становится бесконечно большим (окружность превращается в прямую), получаем циклоиду (см.) при , когда подвижная окружность обращения в прямую, получаем эвольвенту круга (см. Эвольвенты). Частным случаем эпициклоиды является также кардиоида (см.), для которой . При , Г. обращается в прямую, и каждая точка движется по диаметру неподвижной окружности; этим иногда пользуются при конструировании зубчатых сцеплений для превращения кругового движения в прямолинейное (например в некоторых типах печатных машин). Как во всех рулеттах, нормаль всегда проходит через мгновенную точку касания , и, стало быть, прямая есть касательная, но замечательное свойство гипоциклоидов и эпициклоидов состоит в том, что точки и (центр кривизны) гармонически сопряжены с точками и , т. е. центр кривизны в каждой точке лежит на поляре этой точки относительно неподвижной окружности. Из этого следует, что он лежит на том из диаметров неподвижной окружности, к-рый проходит через точку , диаметрально противоположную точке .

















