Парабола (греч.), в геометрии плоская кривая, геометрическое место точек, равноудаленных от неподвижной точки F (фокус) и неподвижной прямой LL (директриса). Если опустим из F перпендикуляр на LL, то средина M расстояния oF принадлежит П., п. ч. oM = MF. Точка M назыв. вершиной П. Расстояние oF, единственная переменная, значениями которой различаются между собой П., называется параметром, а вся прямая oF назыв. осью П. Если точка A принадлежит П., то расстояние A от директрисы должно равняться расстоянию A от фокуса. Отсюда следующее построение П. по точкам: соединим произвольную точку a на LL с F, восставим в a перпендикуляр aX к LL и проведем чрез середину aF перпендикуляр (ось симметрии) tA, который пересечет aX в A. П. симметрично расположена относительно оси oF и удаляется в бесконечность по мере того, как точка a движется в обе стороны по LL. Прямые aX, параллельные оси, наз. диаметрами. Ось симметрии ta касается П. в A и наз. 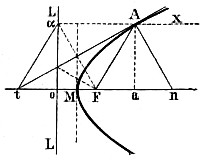 касательною, потому что для всякой иной точки ее, напр. B, Ba = aF, но Ba, как гипотенуза, больше перпендикуляра, опущенного из B на LL. Расстояние FA назыв. радиус-вектор или вектор A, перпендикуляр An к касательной в точке A наз. нормаль; перпендикуляр Aa ордината y точки A и Ma — абсцисса, an — поднормаль. Прямая может иметь с П. только две общие точки, след. П. кривая 2 порядка или коническое сечение, при том с эксцентрицитетом e = 1. П. получается при сечении конуса плоскостью, параллельною производящей. Четыреугольник taAF — ромб, отсюда: 1) поднормаль an постоянная и равна параметру; 2) F одинаково отстоит от A, t и n; поэтому для проведения касательной и нормали достаточно описать радиусом FA круг, который засечет ось в t и n, и соединить t и n с A; 3) так как Mt = Ma, то , где p параметр; 4) касательная в вершине П. делит пополам все касательные между осью и П.; 5) нормаль делит пополам угол между диаметром и радиусом-вектором (∠ XAn = ∠ AnF, как внутренние накрест лежащие, и ∠ FAn = ∠ anF, как углы при основании равнобедренного треугольника с вершиной F). Вообще П. наз. кривые, выражаемые уравнениями: или ; так напр. полукубическая П., открытая английским математиком Уильямом Нейлем (1637—1670) выражается уравнением: .
касательною, потому что для всякой иной точки ее, напр. B, Ba = aF, но Ba, как гипотенуза, больше перпендикуляра, опущенного из B на LL. Расстояние FA назыв. радиус-вектор или вектор A, перпендикуляр An к касательной в точке A наз. нормаль; перпендикуляр Aa ордината y точки A и Ma — абсцисса, an — поднормаль. Прямая может иметь с П. только две общие точки, след. П. кривая 2 порядка или коническое сечение, при том с эксцентрицитетом e = 1. П. получается при сечении конуса плоскостью, параллельною производящей. Четыреугольник taAF — ромб, отсюда: 1) поднормаль an постоянная и равна параметру; 2) F одинаково отстоит от A, t и n; поэтому для проведения касательной и нормали достаточно описать радиусом FA круг, который засечет ось в t и n, и соединить t и n с A; 3) так как Mt = Ma, то , где p параметр; 4) касательная в вершине П. делит пополам все касательные между осью и П.; 5) нормаль делит пополам угол между диаметром и радиусом-вектором (∠ XAn = ∠ AnF, как внутренние накрест лежащие, и ∠ FAn = ∠ anF, как углы при основании равнобедренного треугольника с вершиной F). Вообще П. наз. кривые, выражаемые уравнениями: или ; так напр. полукубическая П., открытая английским математиком Уильямом Нейлем (1637—1670) выражается уравнением: .
БЭЮ/Парабола, в геометрии
< БЭЮ
| ← Парабановая кислота | Парабола | Парабола, в литературе → |




