Страница:БСЭ-1 Том 33. Классы - Конкуренция (1938)-1.pdf/174

Так как крутизна характеристики есть величина переменная, зависящая от $v$, то полученное нами уравнение нелинейно. Общих методов для решения нелинейных дифференциальных уравнений, как известно, не существует. Для полученного нами уравнения при нек-рых существенных ограничениях могут быть найдены приближенные решения. Именно, если сопротивление $R$ контура достаточно мало, приближенное решение уравнения (6) есть гармонии, функция с угловой частотой $\omega _{0}$, но уже не с произвольной, а с вполне определенной амплитудой (или одной из нескольких вполне определенных амплитуд), зависящей не от начальных условий, а от параметров самой системы.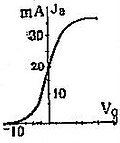Рис. 6 Но для того, чтобы такое решение было возможно, коэффициент взаимной индуктивности $M$ должен быть определенного знака и больше некоторого критич. значения, т. е. обратная связь должна быть определенного направления и достаточно сильной. Этот результат легко поддается физич. истолкованию с точки зрения баланса энергии в системе. В течение нек-рой части периода (когда $MS>RC$) в контур может поступать больше энергии, чем за это время в нем теряется, т. е. контур в это время ведет себя так, как будто он обладает «отрицательным сопротивлением». В течение другой части периода (когда $MS<RC$) потери энергии в контуре больше, чем поступление энергии из анодной цепи, и контур ведет себя как обычный контур с положительным сопротивлением. И если в среднем за период (только в среднем за период, а не в каждый отдельный момент) сопротивление равно нолю, то в контуре происходят стационарные К. Значит, для того чтобы были возможны стационарные К., сопротивление системы должно изменяться; система должна обладать переменным сопротивлением, зависящим от ее состояния, значит, она должна быть нелинейной.

Этот вывод, сделанный нами на основании очень упрощенных и не строгих рассуждений для одного только частного случая, может быть строго обоснован и обобщен на все автоколебательные устройства. Для того чтобы система могла совершать стационарные К. с амплитудой, не зависящей от начальных условий, она должна обладать нелинейностью определенного типа в диссипативных членах, т. е. параметры системы, характеризующие потери энергии в ней, должны известным образом зависеть от состояния системы. В простейшем случае, как мы видели, это сводится к тому, что сопротивление системы в нек-рой области ее состояний должно становиться отрицательным. В обоих рассмотренных нами примерах автоколебательных систем, помимо источника энергии и регулирующего механизма, можно выделить еще одну часть — «собственно» колебательную систему. В часах этой системой является маятник, а в ламповом генераторе — колебательный контур $L_{1}C$. Наличие такой колебательной системы, способной в отсутствии источника энергии и регулирующего механизма совершать свободные затухающие колебания, не является обязательным для автоколебательных устройств. Существуют и такие автоколебательные устройства, в к-рых нет никаких частей, способных совершать свободные К. Но присутствие колебательной системы сообщает автоколебательному устройству некоторые весьма существенные и полезные в большинстве случаев черты и, в частности, позволяет легко получить близкие к синусоидальным К., а это часто бывает очень важно.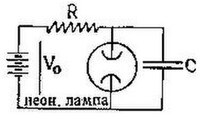Рис. 7Рис. 8 Период этих автоколебаний обычно близок к периоду свободных К., к-рые могут происходить в системе в отсутствии источника энергии и регулирующего механизма. Такие системы принято сейчас называть «томсоновскими», т. к. период их примерно определяется той же формулой Томсона, к-рой определяется период свободных К. в колебательном контуре. Системы же «не томсоновские», т. е. лишенные колебательных контуров, обычно совершают автоколебания, существенно отличные от синусоидальных. Период этих автоколебаний часто приближенно определяется т. н. временем релаксации (в механике временем релаксации называют время, характеризующее скорость исчезновения упругих деформаций в среде, обладающей большой вязкостью; по аналогии, в области электрич. явлений временем релаксации принято называть, напр., время, характеризующее скорость разряда конденсатора через сопротивление). Это дало повод называть К. такого типа «релаксационными». Типичным примером системы,, создающей релаксационные К. («релаксационной системы»), может служить схема с неоновой лампой (рис. 7). Характерная «пилообразная» форма колебаний, создаваемых этой схемой, приведена на рис. 8. Частота этих колебаний существенно зависит от режима схемы (величины $V_{0}$).

При неизменном режиме частота автоколебаний обратно пропорциональна произведению $RC$.

Рассматривая проблему возникновения К. в автономных системах, мы пока ограничивались только системами с одной степенью свободы. Но и по отношению к системам со многими степенями свободы, а также и системам с «распределенными параметрами» или сплошным системам справедливы все основные положения, высказанные выше, а именно: в консервативных системах возможны стационарные К., но с амплитудами, целиком зависящими от начальных условий. В диссипативных системах происходят только затухающие К., и стационарные К. невозможны. В нелинейных системах с нелинейностью определенного типа в членах, характеризующих рассеяние энергии в системе, возможны автоколебания, т. е. стационарные К. с амплитудой, не зависящей от начальных условий. Однако самый характер К., возникающих в системах со многими степенями свободы, может существенно отличаться от К. в системах с одной степенью свободы.

Рассмотрим в качестве примера систему с двумя степенями свободы, изображенную на рис. 9, т. е. две массы $m_{1}$ и $m_{2}$, укрепленные на пружинах. Эту систему удобно рассматривать, как две связанных системы. Однако для дальнейшего это не существенно, и все основные выводы, будут справедливы для всякой системы с двумя степенями свободы, а не только для таких устройств, к-рые можно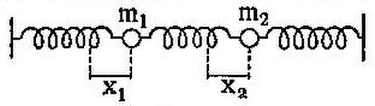Рис. 9 рассматривать как две связанные системы. Только нужно будет все сказанное относить не к координатам двух систем, а к двум координатам одной и той же системы. Ограничимся достаточно малыми отклонениями шариков $m_{1}$ и $m_{2}$ так, чтобы пружины можно было бы считать подчиняющимися закону Гука. Кроме того, положим для простоты, что оба шарика имеют одинаковую массу $m$ и все три пружины — одинаковую упругость $k$. Тогда для движения обоих шариков мы получим на основании второго закона Ньютона следующие уравнения:

$m{\frac {d^{2}x_{1}}{dt^{2}}}=-kx_{1}+k(x_{2}-x_{1})$ и $m{\frac {d^{2}x_{2}}{dt^{2}}}=-kx_{2}+k(x_{1}-x_{2})$

или $m{\frac {d^{2}x_{1}}{dt^{2}}}+2kx_{1}-kx_{2}=0$; $m{\frac {d^{2}x_{2}}{dt^{2}}}+2kx_{2}-kx_{1}=0$,

(7)

где $x_{1}$ и $x_{2}$ — смещения обоих шариков относительно положений равновесия. Общие решения этой системы уравнений имеют вид:

$x_{1}=A\cos {({\sqrt {\frac {k}{m}}}t+\varphi _{1})}+B\cos {({\sqrt {\frac {3k}{m}}}t+\varphi _{2})}$ $x_{2}=A\varkappa _{1}\cos {({\sqrt {\frac {k}{m}}}t+\varphi _{1})}+B\varkappa _{2}\cos {({\sqrt {\frac {3k}{m}}}t+\varphi _{2})}$,

где $\varkappa _{1}$ и $\varkappa _{2}$ — т. н. коэффициенты распределения, определяемые параметрами системы. Начальными условиями определяются только константы $A$ и $B$, а коэффициенты $\varkappa _{1}$ и $\varkappa _{2}$ определяются параметрами системы. Это значит, что начальными условиями мы можем, напр., задать любое распределение амплитуд обоих К. одного шарика, но тогда распределение амплитуд обоих К. другого шарика будет уже вполне определенным. При наличии начальных отклонений или начальных толчков оба шарика будут совершать К., но уже не гармонические, а более сложного характера. Каждый шарик совершает К., к-рые, вообще говоря, представляют собой сумму двух гармонич. К. с различными периодами. Как и в случае линейной системы, с одной степенью свободы, период этих К. определяется свойствами системы, а амплитуды и фазы: обоих К. — начальными условиями. Однако отношение амплитуд непроизвольно и определяется параметрами системы. В частности, можно выбрать начальные условия так, чтобы первый шарик совершал только одно из двух гармонич. К.; для этого достаточно оба шарика отклонить одинаково в одну сторону или в разные стороны. Тогда и второй шарик будет совершать только то же самое гармонии. К., которое совершает первый. Вообще же говоря, каждый шарик будет одновременно совершать оба гармонии. К. Эти гармонич. К., из к-рых состоит движение каждого из шариков, носят название