Луна — спутник Земли, ближайшее к нам небесное тело. Среднее расстояние Л. от Земли равно 60,27 экваториальным радиусам Земли. Средний экваториальный горизонтальный параллакс (см.) Л. — 57′2.3″, что соответствует расстоянию около 385000 км. Вследствие эллиптичности лунного пути около Земли (эксцентриситет для 1850,0 года = 0,054908) и вследствие притягательного действия Солнца расстояние Л. от Земли изменяется в течение ее оборота около Земли, причем наибольшее расстояние Л. от Земли равно 407110 км, а наименьшее 356650 км. При среднем расстоянии диаметр лунного диска усматривается с Земли под углом в 31′8′, этот диаметр равен, следовательно, 3480 км. Принимая массу, поверхность, объем и плотность Земли за единицы, эти величины для Л. соответственно будут 0,0123, 0,0745, 0,0203 и 0,604. Видимое движение Л. совершается в поясе созвездий зодиака (см. XII, 624) с З. на В. Если видимый путь Л. построить на небесной сфере, приняв за центр сферы центр Земли, то получится почти большой круг, пересекающий эклиптику (см.) в двух точках; та из этих точек, по направлению к которой усматривается Л. при переходе ее с южной стороны эклиптики на северную, называется восходящим углом 
(долгота восходящего угла для 1850.0 г. = 146°13′40″), другая же — нисходящим 
, линия же, их соединяющая, — линией узлов; таким образом движение Л. совершается в плоскости, проходящей через центр Земли; эта плоскость наклонена к плоскости эклиптики под углом в 5° 8′ 40″ (в среднем для 1850,0 года). Среднее движение Л. по долготе составляет 13° 10′ 35″ в одни средние сутки, так что через 27,321582 средних суток Л. возвращается к прежней ее долготе, этот период называется тропическим месяцем; полный же оборот Л. около Земли, называемый звездным месяцем, равен 27,321661 средним суткам. Истинный путь или орбита Л. около Земли сходен с эллипсом, в одном из фокусов которого находится центр Земли. Большая полуось этого эллипса называется линией апсид; ближайшая к Земле точка лунной орбиты называется перигеем, а наиболее удаленная — апогеем (долгота перигея для 1850,0 года = 99° 51′ 52″). Долгота восходящего узла, наклонность, долгота перигея, a также эксцентриситет лунной орбиты и среднее расстояние Л. от Земли подвержены изменениям; долгота восходящего узла лунной орбиты уменьшается при этом весьма неодинаково, в среднем же приблизительно на 19° 20′,5 в год, поэтому линия узлов описывает полную окружность приблизительно в 18,6 лет. Вследствие отступления линии узлов лунной орбиты период возвращения Л. к одному и тому же узлу менее полного оборота ее около Земли этот период называется драконическим месяцем и равен 27,2122 средн. сут. Название «драконический» объясняется тем, что древние представляли себе дракона, подстерегавшего Л. вблизи эклиптики и иногда заслонявшего ее собой: тогда происходило, по представлению древних, затмение (см. XII, 327). Наклонность лунной орбиты периодически изменяется в пределах от 5° до 5° 15′; период этого изменения тоже приблизительно 18,6 лет. Долгота перигея постоянно увеличивается, в среднем приблизительно на 40°41′,4 в год, поэтому линия апсид описывает полную окружность в 8,8 года. Период возвращения Л. к перигею называется аномалистическим месяцем и равен 27,5546 средн. сут. Параллакс (см.) Л. в перигее изменяется в пределах от 59′ 23″ до 1° 1′ 24″, а в апогее от 52′ 40″ до 54′ 12″.
Изменения вида Л., обусловливаемые положениями ее относительно Солнца и Земли, носят назв. фаз Л. Когда Л. находится в соединении с Солнцем и, следовательно, проходит через меридиан одновременно с ним, Л. обращена к нам неосвещенной стороной — эта фаза называется новолунием. Дня через два после новолуния Л. усматривается к В. от Солнца в виде узкого серпа, обращенного выпуклостью в сторону Солнца; приблизительно через 7 дней после новолуния наступает первая четверть — освещена правая половина лунного диска; угол при Л. между направлениями на Землю и на Солнце делается тогда равным 90°. Л. проходит через меридиан приблизительно в 6 час. вечера. После первой четверти прохождения Л. через меридиан происходят все позднее и позднее, и приблизительно через 14 дней после новолуния наступает полнолуние — Л. проходит через меридиан приблизительно в полночь, она находится в противостоянии с Солнцем и представляется в виде светлого круглого диска. После полнолуния освещенная часть Л. уменьшается и в последней четверти, через 7 дней после полнолуния, освещена лишь левая половина лунного диска, угол при Л. между направлениями на Землю и на Солнце при этом опять 90°, Л. находится к З. от Солнца и проходит через меридиан приблизительно в 6 час. утра. После последней четверти освещенная часть диска уменьшается с каждым днем, и Л. представляется опять в виде серпа. Новолуние и полнолуние называются сизигиями, первая и последняя четверть — квадратурами. Фазы Л. доказывают, что она есть тело темное, освещаемое лишь солнечными лучами. Когда Л. представляется в виде узкого серпа, то бывает видна обыкновенно и остальная часть ее диска в слабом сероватом блеске, что называют пепельным светом: он наблюдается простым глазом уже дня два спустя или дня за два пред новолунием. Верное объяснение пепельного света (он происходит вследствие отражения на Л. солнечных лучей от поверхности Земли) Кеплер приписывает своему учителю Местлину (1596), хотя это объяснение дал уже Леонардо да Винчи. Когда новолуние или полнолуние случается вблизи одного из узлов лунной орбиты, то происходит в первом случае солнечное, а во втором лунное затмение (см. Затмения). Период возвращения Л. к одной и той же фазе называется синодическим месяцем и равен в среднем 29,530589 средн. сут. Между вышеприведенными лунными месяцами, или оборотами, существует следующее соотношение: 241 звездных, или тропических, месяцев = 242 драконическим месяцам = 239 аномалистич. месяцам = 223 синодическим месяцам = 18 годам и 10,5 дням. Этот период, известный уже древним и называемый Сарос, может служить для приблизительного предсказания затмений Солнца и Л. (см. Затмения). Возвращение Л. к прежним ее фазам имело и имеет большое значение в жизни всех народов: древние в дни новолуний и полнолуний совершали известные обряды; по правилам христианской церкви Пасха празднуется всегда в воскресенье, следующее за первым полнолунием после весеннего равноденствия; у евреев, магометан и китайцев лунный год положен в основу календаря. Поэтому понятно, как важно было знать соотношение между длиной тропического года (см. IX, 35) и синодического месяца. Еще древними астрономами Вавилона было найдено и в 433 г. до Р. Хр. передано Метоном грекам, что в 19 годах содержится ровно 235 лунных месяцев. Этот период в 19 лет назыв. кругом или циклом Л.; за начало лунного цикла принимается тот год, когда новолуние совпадает с началом года (1 января); порядок годов в лунном цикле определяется числами от 1 до 19, которые называются золотыми числами; название «золотое число» объясняется тем, что, по свидетельству некоторых писателей, греки написали открытие Метона золотыми буквами на общественных памятниках.
Вследствие притяжения Л. Солнцем и планетами, вследствие эллиптичности земной орбиты и сжатия Земли возмущения (см. VI, 891) в движении Л. весьма значительны. Выше было уже сказано, как быстро происходят вековые (пропорциональные времени) изменения в долготе восходящего узла лунной орбиты и долготе ее перигея. Наклонность лунной орбиты к эклиптике и ее эксцентриситет подвержены только периодическим изменениям. Весьма замечательную аномалию в движении Л. представляет ускорение ее среднего движения, производящее с течением времени весьма значительное изменение в долготе Л. Это вековое неравенство было открыто еще в начале XVIII ст. Галлеем из сравнения древнейших наблюдений с наблюдениями его времени. На основании общей теории притяжения в средней скорости движения Л. не должно было бы происходить вековых изменений, поэтому следовало найти объяснение открытия Галлея. Это удалось лишь Лапласу, который показал, что причина ускорения среднего движения Л. лежит в временном уменьшении эксцентриситета земной орбиты (maximum эксцентриситета земной орбиты был 0,01965 в 11448 г. до Р. Хр., после того времени он уменьшается и достигнет minimum’a 0,00393 в 25410 г.) и нашел, ограничиваясь первым приближением, теоретически, что вследствие указанной причины средняя долгота Л. должна увеличиваться на 10″,2 x τ2, означая через τ число веков, протекших с 1800 г. Найденная Лапласом теоретическая величина удовлетворительно согласуется с величиной 12″,2 x τ2, выведенной Ганзеном из наблюдений древних затмений; таким образом, казалось, что теория удовлетворительно объясняет величину ускорения среднего движения Л. Но в 1853 г. появился мемуар Адамса, который повел вычисление Лапласа дальше и показал, что коэффициент векового ускорения в среднем движении Л. равен лишь 6″; ту же величину получил и Делоне, произведший самостоятельные вычисления. Таким образом, принимая вывод Адамса, оказывается разность между вычисленным и наблюденным ускорением; возможную же причину этой разности Адамс и Делоне видели в замедлении вращения Земли около оси. Для объяснения разности между наблюденным ускорением Л. и вычисленным достаточно бы было принять, что замедление вращения Земли за последние 2000 лет составляет лишь 0,012 сек., чего мы не в состоянии обнаружить наблюдением. Следует заметить, однако, что пока не будет решен вопрос о достаточности формул, употребляемых ныне для вычисления возмущений, все другие предположения о причине ускорения среднего движения Л. преждевременны; известно, что первоначальные вычисления движения линии апсид лунной орбиты заставили было Клеро усомниться в достаточности закона всемирного тяготения для объяснения этого движения, но дальнейшие его вычисления показали, что теория уже лучше согласуется с наблюдением и в настоящее время наблюдаемое движение перигея лунной орбиты вполне объясняется теоретически. Из множества возмущений в движении Л. важнейшие — эвекция (см.), вариация (см. V, 525) и годичное неравенство, которое имеет периодом аномалистический год (см. IX, 35), maximum его ±11′12″, т. е. настолько истинная долгота Л. может отличаться от средней. Эти возмущения носят название больших лунных неравенств и были найдены из наблюдений долготы Л. уже давно, первое еще Птолемеем, а второе и третье Тихо Браге; объяснены же эти неравенства по теории тяготения в первый раз Ньютоном. Остальные меньшие возмущения в движении Л. были выведены подробными исследованиями Лапласа, Ганзена, Делоне и др., из них наиболее значительное — параллактическое неравенство, имеющее периодом синодический месяц и зависящее от отношения параллаксов Солнца и Л.; поэтому, будучи выведено по величине из наблюдений, это неравенство дает возможность вычислить параллакс Солнца: так Ганзен нашел солнечный параллакс 8″,916. Еще замечательно возмущение в широте Л. с месячным периодом, зависящее от сжатия Земли; это неравенство, будучи выведено по величине из наблюдений, дает возможность найти сжатие Земли, так Лаплас получил сжатие Земли 1/305. Теорией поступательного движения Л. около Земли занимались величайшие геометры и астрономы, начиная с Ньютона (Ньютон, Клеро, Даламбер, Эйлер, Лаплас, Пуассон, Делоне, Адамс, Ганзен, Гюльден), что объясняется громадным интересом вопроса, так как в приложении к исследованию движения Л. лучше всего выясняются достоинства того или другого способа вычисления возмущений; кроме того, наблюдения указывают на существование неравенств, которые предстоит еще вывести теоретически. Директор парижской обсерватории Тиссеран собрал почти все исследования по теории движения Л. в третьем томе своего «Traité de mécanique céleste» (П., 1894). На основании теории вычисляются таблицы Л., которые служат для определения места ее на небесном своде в любой момент времени; такие таблицы, называемые лунными, были впервые составлены Галлеем и Эйлером; позднее Тобиас Майер дал таблицы, представлявшие движение Л. с точностью до 1. Бургхард составил таблицы на основании теории Лапласа; уклонения этих таблиц доходили до 40″; еще более точные таблицы были даны Карлини, Плана и Дамуазо. Самыми же точными лунными таблицами считаются до сих пор таблицы Ганзена, изданные в 1857 г. на счет английского правительства; однако теперь эти таблицы уже расходятся с наблюдениями; к вычисленным по таблицам Ганзена положениям Л. придаются в настоящее время эмпирические поправки по Ньюкомбу; в будущем предстоит составить новые таблицы, так как таблицы Ганзена представляют движение Л. лишь за время с 1760 по 1850 г., после же и до этого времени они расходятся с наблюдениями. Движение Л. представляет еще ту особенность, что относительный путь Л. около Солнца есть кривая, обращенная всюду вогнутостью к Солнцу и не имеющая ни точек перегиба, ни точек возврата; орбиты же около Солнца всех прочих известных нам спутников планет представляют бесконечный ряд тех или других точек.
Л. вращается ок. своей оси в ту же сторону и с той же средней угловой скоростью, с какой обходит вокруг Земли, что следует из того всем известного факта, что Л. обращена к Земле всегда одной и той же половиной; таким образом, продолжительность полного оборота Л. около ее оси равна 27,3217 ср. сут., а угловая скорость вращения 13° 10′ 35″. Лунный экватор наклонен к эклиптике под углом в 1° 32′, а восходящий узел его постоянно совпадает с нисходящим узлом лунной орбиты и, следов., совершает полный оборот в 18,6 лет; это постоянное отступление восходящего узла лунного экватора можно назвать лунной прецессий (см. Прецессия). Чтобы объяснить лунную прецессию и совпадение времени оборотов Л. около оси и около Земли, следует считать Л. не шаром, а растянутым, по направлению к Земле, эллипсоидом. Ганзен показал, что для объяснения некоторых неравенств движения Л. следует допустить, что центр тяжести Л. отстоит от нас приблизительно на 59 км. далее ее центра. Так как вращение Л. около ее оси совершается равномерно, а движение ее вокруг Земли происходит неравномерно (наибольшую скорость Л. имеет в перигее, а наименьшую в апогее), то угол, на который поворачивается Л. в течение некоторого времени, выходит то больше, то меньше той дуги, которую Л. пройдет в то же время по своей орбите около Земли, вследствие этого нам будет открываться несколько более то правая, то левая сторона Л. Это кажущееся колебание Л. около линии, соединяющей центр Л. и Солнца, носит название либрации по долготе (maximum ее 7°54′); так как ось вращения Л. не вполне перпендикулярна к плоскости ее орбиты, а уклоняется от этого положения на 1°32′, то происходит еще небольшое кажущееся колебание Л. в направлении перпендикулярном к эклиптике, которое называется либрацией по широте (maximum ее 6° 51′). Кроме этого существует еще так назыв. параллактическая либрация, происходящая от того, что мы наблюдаем Л. не из центра Земли, а с ее поверхности. Вследствие всех указанных причин мы можем видеть более половины Л., именно около 0,59. В общем наибольшая либрация составляет 11°25′. Едва заметное действительное колебание оси вращения Л. называется физической либрацией.
Уже невооруженный глаз различает на Л. темные пятна; в трубу же усматривается много подробностей рельефа лунной поверхности. Хотя уже Галилей, рассматривая Л. в устроенный им телескоп с увеличением в 30 раз, показал, что Л. покрыта горами, и даже измерил высоты лунных гор по величине их теней, однако за первого селенографа, по справедливости, следует считать Гевелия, которого карты и описание лунной поверхности имели долго научное значение. В конце прошлого столетия особенное значение в селенографии имели работы Шретера (Schröter), утратившие свое значение лишь с появлением карт Л., составленных Лорманом, Беером и Медлером. Позднее появились классические труды Нейсона (E. Neison, «The moon and the conditions and configurations of its surface», 1876); есть и немецкий перевод Клейна и Шмидта («Charte der Gebirge des Mondes, nach eigenen Beobachtungen in den Jahren 1840—74 entworfen», 1878). В настоящее время делаются прекрасные фотографии Л. в Ликовской обсерватории, увеличиваемые затем Вейнеком в Праге, фотографируют Л. также братья Анри (Henry) в Париже, Принц в Брюсселе и др., а в Англии существует целое селенографическое общество, имеющее целью изучение Л. Желающим ознакомиться с топографией Л. можно рекомендовать книгу Elger’a («The moon. A full description and map of its principal physical features», 1895) и на русском языке «Путеводитель по небу» Покровского (1894). Различные образования лунной поверхности подразделяются на четыре главные группы: долины (maria, palus, lacus, sinus), кратеры, горы (цирки) и трещины (Rillen). Большинство морей (под этим названием разумеются большие темные пространства) находятся в северной части лунной поверхности, названия главнейших из них, идя от З. к В., суть: M. Crisium, Foecunditatis, Nectaris, Tranquillitatis, Serenitatis, Vaporum, Frigoris, Imbrium, Nubium, Humorum и Oceanus Procellarum (см. прилож. карту Л.).
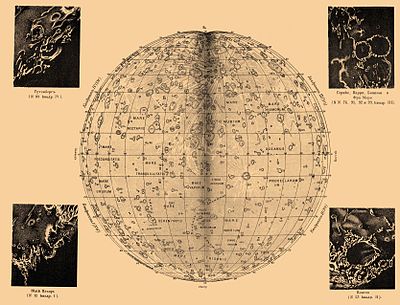
| I. Квадрант (NW) | II. Квадрант (NO) | III. Квадрант (SO) | IV. Квадрант (SW) |
|---|---|---|---|
| 1. Шуберт. | 1. Паллас. | 1. Малаперт. | 1. Шомбергер. |
| 2. Непер. | 2. Боде. | 2. Кабеус | 2. Симпелиус. |
| 3. Фирмикус | 3. Шретер. | 3. Шорт. | 3. Богуславский. |
| 4. Аполлоний. | 4. Гамбар. | 4. Моретус. | 4. Буссенго. |
| 5. Тарунций. | 5. Стадиус. | 5. Ньютон. | 5. Манзинус. |
| 6. Максилайн. | 6. Коперник. | 6. Казатус. | 6. Мутус. |
| 7. Сэбин. | 7. Рейнгольд. | 7. Клапрот. | 7. Пентланд. |
| 8. Риттер. | 8. Гортензий. | 8. Вильсон. | 8. Курций. |
| 9. Дионисий. | 9. Энке. | 9. Груембергер. | 9. Понтекулан. |
| 10. Араго. | 10. Кеплер. | 10. Цизатус. | 10. Ханно. |
| 11. Созиген. | 11. Рейнер. | 11. Бланканус. | 11. Биела. |
| 12. Юлий Цезарь. | 12.Гевелий. | 12. Шейнер. | 12. Хагециус. |
| 13. Ариадеус. | 13. Кавалериус | 13. Кирхер. | 13. Нирч. |
| 14. Годен. | 14. Ольберс. | 14. Беттинус. | 14. Розенберг. |
| 15. Агриппа. | 15. Марко Поло. | 15. Бальи | 15. Влак. |
| 16. Боскович. | 16. Эратосфен. | 16. Хаузен. | 16. Хоммель. |
| 17. Гигинус. | 17. Гей-Люссак. | 17. Цукки. | 17. Питискус. |
| 18. Ретикус. | 18. Майер. | 18. Клавий. | 18. Бэкон. |
| 19. Триеснекер. | 19. Милихий | 19. Делюк. | 19. Якоби. |
| 20. Укерт. | 20. Марий. | 20. Магинус. | 20. Цах. |
| 21. Кондорсе. | 21. Бессарион. | 21. Лонгомонтан. | 21. Лилий. |
| 22. Ганзен. | 22. Кардан. | 22. Рост. | 22. Окен. |
| 23. Альгазен. | 23. Крафт | 23. Вейгель. | 23. Вега. |
| 24. Озу. | 24. Гюйгенс. | 24. Сегнер. | 24. Штейнгель. |
| 25. Пикар. | 25. Вольф. | 25. Байер. | 25. Фабриций. |
| 26. Проклус. | 26. Архимед. | 26. Шиллер. | 26. Николаи. |
| 27. Жансен. | 27. Тимохарис. | 27. Фоциклид. | 27. Клеро. |
| 28. Витрувий. | 28. Питеас. | 28. Варгентин. | 28. Бароциус. |
| 29. Маральди. | 29. Ламберт. | 29. Соссюр. | 29. Мавролик. |
| 30. Плиний. | 30. Эйлер. | 30. Пикте. | 30. Кювье. |
| 31. Росс. | 31. Диофант. | 31. Стрит. | 31. Лицетус. |
| 32. Ахеризия. | 32. Лагир. | 32. Тихо Браге. | 32. Штефлер. |
| 33. Таке. | 33. Геродот. | 33. Вильгельм I. | 33. Маринус. |
| 34. Менелай. | 34. Селевк. | 34. Гейнзиус. | 34. Фрауенгофер. |
| 35. Сульпиций. | 35. Бриггс. | 35. Хейнцель. | 35. Фурнериус. |
| 36. Манилий. | 36. Аристарх. | 36. Дреббель. | 36. Стевин. |
| 37. Агарум. | 37. Геликон. | 37. Шикард. | 37. Рейта. |
| 38. Эймарт. | 38. Карлини. | 38. Ингирами. | 38. Меций. |
| 39. Ориани. | 39. Делиль. | 39. Леман. | 39. Рейхенбах. |
| 40. Плутарх. | 40. Волластон. | 40. Наср-Эддин. | 40. Неандр. |
| 41. Сенека. | 41. Лихтенберг. | 41. Оронтиус. | 41. Стибориус. |
| 42. Хан. | 42. Лавуазье. | 42. Сассерид. | 42. Риччи. |
| 43. Бероз. | 43. Кирх. | 43. Лексель. | 43. Рабби-Леви. |
| 44. Клеомед. | 44. Пико | 44. Вальтер. | 44. Загут. |
| 45. Траллес. | 45. Лаплас. | 45. Хелль. | 45. Линденау. |
| 46. Макробий. | 46. Гераклид. | 46. Гаурик. | 46. Бюшинг. |
| 47. Ромер. | 47. Мопертюи. | 47. Вурцельбауер. | 47. Бух. |
| 48. Литров. | 48. Бианкини. | 48. Питатус. | 48. Гемма-Фризиус. |
| 49. Лемонье. | 49. Шэрп. | 49. Гезиод. | 49. Пуассон. |
| 50. Бессель. | 50. Меран. | 50. Цихус. | 50. Алиацензис. |
| 51. Линней. | 51. Лувилль. | 51. Капуан. | 51. Гумбольд. |
| 52. Конон. | 52. Герард. | 52. Рамсден. | 52. Гекатей. |
| 53. Гадлей. | 53. Платон. | 53. Вителло. | 53. Лежандр. |
| 54. Брадлей. | 54. Лакондамин. | 54. Пиацци. | 54. Петавий. |
| 55. Гаусс. | 55. Бугер. | 55. Лагранж. | 55. Снеллиус. |
| 56. Буркгардт. | 56. Гарпал. | 56. Бувар. | 56. Борда. |
| 57. Геминус. | 57. Энопид. | 57. Региомонтан. | 57. Фракастор. |
| 58. Бернулли. | 58. Репсольд. | 58. Пурбах. | 58. Сантбек. |
| 59. Мессала. | 59. Хардинг. | 59. Тебит. | 59. Пикколомини. |
| 60. Берцелиус. | 60. Ксенофан. | 60. Меркатор. | 60. Полибий. |
| 61. Франклин. | 61. Клеострат. | 61. Кампанус. | 61. Понс. |
| 62. Поссидоний. | 62. Тимеус. | 62. Гиппалус. | 62. Фермат. |
| 63. Калипп. | 63. Эпиген. | 63. Кис. | 63. Сакробоско. |
| 64. Феатетус | 64. Фонтенель. | 64. Биллиальд. | 64. Понтанус. |
| 65. Аристиль. | 65. Горребоу. | 65. Доппельмайер. | 65. Азофи. |
| 66. Автолик. | 66. Анаксимандр. | 66. Фурье. | 66. Абанецца. |
| 67. Кассини. | 67. Пифагор. | 67. Вьет. | 67. Апиан. |
| 68. Струве. | 68. Джойа. | 68. Кавендиш. | 68. Плайфер. |
| 69. Шумахер. | 69. Анаксагор. | 69. Биргиус. | 69. Вернер. |
| 70. Меркурий. | 70. Филолай. | 70. Мерсен. | 70. Ансгариус. |
| 71. Гук. | 71. Анаксимен. | 71. Эйхштедт. | 71. Венделин. |
| 72. Цефей. | 72. Галилей. | 72. Арзахель. | 72. Кук. |
| 73. Эрштед. | 73. Альфонс. | 73. Колумб. | |
| 74. Атлас. | 74. Альпетрагий. | 74. Магелан. | |
| 75. Геркулес. | 75. Деви. | 75. Боненбергер. | |
| 76. Мазон. | 76. Герике. | 76. Элиде-де-Бомон. | |
| 77. Плана. | 77. Лубинецкий. | 77. Феофил. | |
| 78. Бюрг. | 78. Агатархид. | 78. Св. Кирилл. | |
| 79. Евдокс. | 79. Гассенди. | 79. Св. Екатерина. | |
| 80. Аристотель. | 80. Летрон. | 80. Кант. | |
| 81. Эгеде. | 81. Бейли. | 81. Тацит. | |
| 82. Эндимион. | 82. Зуп. | 82. Альмамум. | |
| 83. Страбон. | 83. Фонтана. | 83. Гебер. | |
| 84. Фалес. | 84. Сирзалис. | 84. Абул-Вефа. | |
| 85. Гертнер. | 85. Крюгер. | 85. Эйри. | |
| 86. Демокрит. | 86. Рокка. | 86. Альбатегний. | |
| 87. Хр. Майер. | 87. Птолемей. | 87. Паррот. | |
| 88. Метон | 88. Гершель. | 88. Кестнер. | |
| 89. Эвктемон. | 89. Местлин. | 89. Маклорен. | |
| 90. Скоресби. | 90. Лаланд. | 90. Лангрен. | |
| 91. Барроу. | 91. Парри. | 91. Мессие. | |
| 92. Архитас. | 92. Бонплан. | 92. Гоклениус. | |
| 93. Фра Моро. | 93. Гутенберг. | ||
| 94. Ландсберг. | 94. Капелла. | ||
| 95. Эвклид. | 95. Исидор. | ||
| 96. Флемстид. | 96. Торичелли. | ||
| 97. Дамуазо. | 97. Ипатия. | ||
| 98. Гримальди. | 98. Деламбр. | ||
| 99. Лорман. | 99. Гиппарх. | ||
| 100. Риччиоли. | 100. Реомюр. | ||
| 101. Ганстин. | 101. Био. | ||
| 102. Лакайль. | |||
| 103. Декарт. |
Всего насчитывают 14 морей, 8 palus, lacus и sinus. Цвет морей обыкновенно серый, некоторые (М. Humorum и Serenitatis) имеют зеленоватый оттенок. Поверхность морей неровная, в некоторых местах покрыта кратерами. Горы (небольшие — кратеры, большие и широкие — цирки) на Л. напоминают по внешнему их виду наши вулканы; они большей частью круглы, невысоки, но широки. Внутри цирка возвышается одна, иногда две горы. Высоты лунных гор, определяемые по величинам их теней, считаются от уровня окружающей их местности. Самая высокая гора на Л. (у южного полюса — Лейбниц) достигает 7600 м. Вообще лунные горы по высоте не отличаются от земных, но ширина цирков гораздо более ширины земных кратеров. Цирк Clavius имеет в диаметре 210 км. Своей величиной и красотой обращают на себя внимание цирки Plato, Tycho, Aristarchus, Copernicus, Kepler. Самая большая горная цепь на Л. — Апеннины, прилегающая к Mare Imbrium. Как много кратеров на Л., можно судить по тому, что на карте Шмидта нанесено 33000 возвышенностей. Трещины (Rillen) встречаются по всей поверхности Л., иногда они видны и на дне больших цирков; трещины обыкновенно идут по прямым линиям и имеют одинаковую ширину почти на всем их протяжении. В полнолуние хорошо заметны еще на Л. светлые лучи, идущие радиусами из больших ярких центров (напр. из Tycho и Copernicus).
Образование лунных неровностей Фай (Faye) объясняет следующим образом. Некогда Л. находилась в огнежидком состоянии, вследствие притягательного действия Земли на ней происходило явление приливов (см. Прилив), причем высота приливов на Л. должна была доходить до 40 м и даже более. Постепенно охлаждаясь, Л. покрывалась корой; через малые отверстия в коре приливные волны выливались на поверхность и под действием холодного окружающего пространства отвердевали, образуя около отверстий небольшие по высоте валы с широким основанием; эти валы увеличивались по высоте с каждым новым приливом в этом месте; понятно, что приливная волна постепенно уменьшалась, наконец наступал момент, когда и дно отверстий отвердевало. Понятно также, что вследствие трения приливных волн о внутреннюю поверхность коры происходило замедление вращения образовавшейся коры, пока вся масса Л. не отвердела, тогда время оборота Л. около ее оси сделалось равным времени оборота ее вокруг Земли. В недавнее сравнительно время некоторые наблюдатели замечали изменения на поверхности Л.; так, в 1867 г. Шмидт в Афинах заметил перемену в кратере Линнея, лежащем в Mare Serenitatis; Riccioli, Lohrmann и Медлер ясно видели этот кратер, а теперь он почти исчез; один из кратеров Messier (в Mare Foecunditatis) изменил форму и размер со времен Медлера; в последнее время около этого кратера некоторые видели большие трещины и т. п. Возможности изменений на лунной поверхности вследствие сильных изменений температуры на Л. (14-дневный лунный день сменяется там столь же продолжительной ночью ) отрицать нельзя, но следует быть осторожным в заключениях, помня, что вид лунной поверхности зависит от освещения и от увеличения употребляемой трубы. Кроме того, чтобы быть замеченными с Земли, изменения на Л. должны быть громадны. Лишь тщательные и толковые исследования лунной поверхности имеют научное значение.
Наш спутник лишен атмосферы, по крайней мере сравнимой по плотности с нашей; доказательством отсутствия атмосферы на Л. служат: резкость и абсолютная темнота теней лунных гор, мгновенное исчезновение и появление звезд во время покрытия их Л. (см. Затмения), края Л. видны так же отчетливо, как и средина ее диска; наконец, спектр Л. совершенно совпадает со спектром Солнца. Исследования Нейсона не исключают, впрочем, возможности существования атмосферы Л. с плотностью, равной 1/300 плотности нашей. Ганзен допускал существование атмосферы на невидимой нам половине Л. По фотометрическим исследованиям Цельнера, свет Л. в полнолуние в 619000 раз слабее солнечного. Меллони первый, в 1846 г., доказал, что Л. отражает и солнечную теплоту; на основании теоретических соображений, количество теплоты, отражаемой Л., не более 1:280000 той теплоты, которую Земля непосредственно получает от Солнца; такое ничтожное количество теплоты может быть обнаружено лишь помощью термоэлектрических приборов; исследованиями этого рода занимались лорд Росс и Деви. Влияние Л. на Землю наглядно проявляется в приливах и отливах океанов и морей (см. Приливы).