четырехъ прямыхъ перваго пучка всегда будетъ равно ангармоническому отношенію четырехъ прямыхъ во второмъ пучкѣ.
6. Напримѣръ, представимъ себѣ постоянный уголъ; пусть около данной точки, какъ около полюса, вращается прямая линія, которая во всякомъ положеніи будетъ встрѣчаться съ сторонами угла въ двухъ точкахъ. Четыре, опредѣленныя такимъ образомъ, точки на одной изъ сторонъ угла будутъ имѣть одинаковое ангармоническое отношеніе съ четырьмя соотвѣтствующими точками на другой сторонѣ (потому что оба эти отношенія равны ангармоническому отношенію четырехъ сѣкущихъ, служащихъ для опредѣленія этихъ точекъ). Отсюда слѣдуетъ, что, если мы соединимъ какую-нибудь неподвижную точку съ точками, отмѣченными на одной сторонѣ угла, и другую неподвижную точку — съ точками, отмѣченными на другой сторонѣ, то получимъ два пучка соотвѣтствующихъ прямыхъ, пересѣкающихся между собою на коническомъ сѣченіи, проходящемъ черезъ двѣ неподвижныя точки. Итакъ
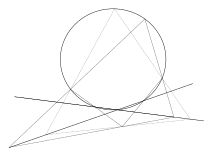
Если три стороны треугольника, измѣняющаго свой видъ, вращаются около трехъ неподвижныхъ точекъ и двѣ вершины его перемѣщаются по двумъ неподвижнымъ прямымъ, то третья вершина описываетъ коническое сѣченіе, проходящее черезъ двѣ точки, около которыхъ вращаются стороны, прилежащія къ этой вершинѣ[1]
- ↑ Если бы сторона треугольника, противолежащая образующей вершинѣ, вмѣсто того, чтобы вращаться около неподвижной точки, cкользила по коническому сѣченію, касающемуся двухъ неподвижныхъ прямыхъ, то свободная вершина треугольника описывала бы также коническое сѣченіе, проходящее черезъ двѣ неподвижныя точки.
Это слѣдуетъ изъ того, что четыре касательныя коническаго сѣченія пересѣкаютъ каждую изъ двухъ другихъ касательныхъ въ четырехъ точкахъ, которыя на той и на другой касательной имѣютъ одинаковое ангармоническое отношеніе (см. слѣдующее Примѣчаніе).
Это обобщеніе теоремы Маклорена и Брайкенриджа можетъ вести ко множеству различныхъ, большею частію новыхъ, предложеній.
четырех прямых первого пучка всегда будет равно ангармоническому отношению четырех прямых во втором пучке.
6. Например, представим себе постоянный угол; пусть около данной точки, как около полюса, вращается прямая линия, которая во всяком положении будет встречаться с сторонами угла в двух точках. Четыре, определенные таким образом, точки на одной из сторон угла будут иметь одинаковое ангармоническое отношение с четырьмя соответствующими точками на другой стороне (потому что оба эти отношения равны ангармоническому отношению четырех секущих, служащих для определения этих точек). Отсюда следует, что, если мы соединим какую-нибудь неподвижную точку с точками, отмеченными на одной стороне угла, и другую неподвижную точку — с точками, отмеченными на другой стороне, то получим два пучка соответствующих прямых, пересекающихся между собою на коническом сечении, проходящем через две неподвижные точки. Итак

Если три стороны треугольника, изменяющего свой вид, вращаются около трех неподвижных точек и две вершины его перемещаются по двум неподвижным прямым, то третья вершина описывает коническое сечение, проходящее через две точки, около которых вращаются стороны, прилежащие к этой вершине[1]
- ↑ Если бы сторона треугольника, противолежащая образующей вершине, вместо того, чтобы вращаться около неподвижной точки, скользила по коническому сечению, касающемуся двух неподвижных прямых, то свободная вершина треугольника описывала бы также коническое сечение, проходящее через две неподвижные точки.
Это следует из того, что четыре касательные конического сечения пересекают каждую из двух других касательных в четырех точках, которые на той и на другой касательной имеют одинаковое ангармоническое отношение (см. следующее Примечание).
Это обобщение теоремы Маклорена и Брайкенриджа может вести ко множеству различных, большею частью новых, предложений.

